Cómo funcionan los circuitos Buck-Boost

Todos hemos escuchado mucho sobre los circuitos buck y boost y sabemos que básicamente estos circuitos se utilizan en diseños SMPS para aumentar o reducir un voltaje dado en la entrada. Lo interesante de esta tecnología es que permite las funciones anteriores con una generación de calor insignificante lo que da como resultado conversiones extremadamente eficientes.

Qué es Buck-Boost, cómo funciona

Aprendamos el concepto en la primera sección sin involucrar muchos tecnicismos para que sea más fácil entender qué es exactamente el concepto de impulso de inversión, incluso para un novato.

Entre las tres topologías fundamentales denominadas buck, boost y buck-boost, la tercera es más popular ya que permite que ambas funciones (buck boost) se utilicen a través de una única configuración simplemente alterando los pulsos de entrada.

En la topología reductora-elevadora, tenemos principalmente un componente de conmutación electrónico que puede tener la forma de un transistor o un mosfet. Este componente se conmuta mediante una señal pulsante de un circuito oscilador integrado.

Aparte del componente de conmutación anterior, el circuito tiene un inductor, un diodo y un condensador como ingredientes principales.

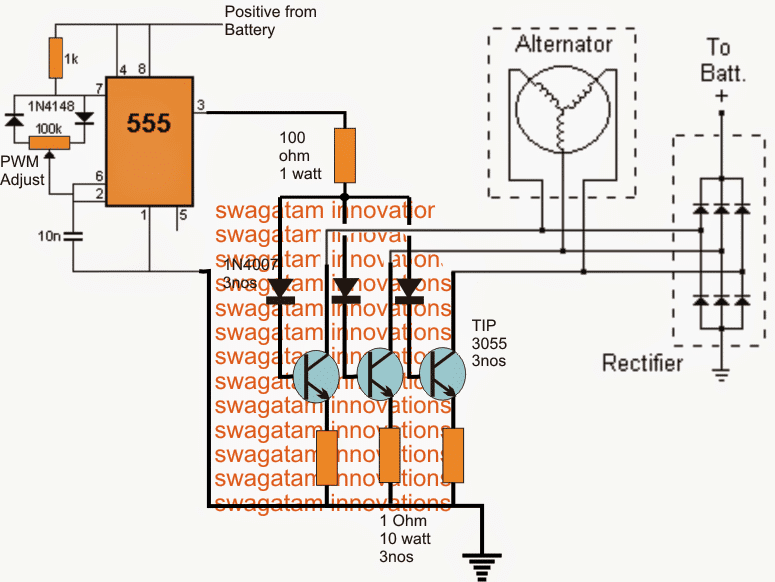
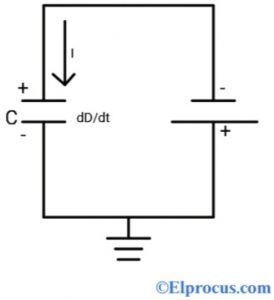
Todas estas partes están ordenadas en la forma que puede verse en el siguiente diagrama:

En referencia al diagrama de refuerzo reductor anterior, el mosfet es la parte que recibe los pulsos que lo obligan a operar en dos condiciones: estado ON y estado OFF.

Durante el estado ON, la corriente de entrada obtiene un camino libre a través del mosfet e instantáneamente intenta atravesar el inductor, ya que el diodo está posicionado en el estado polarizado inverso.

El inductor, debido a su propiedad inherente, intenta restringir la imposición repentina de corriente y, en una respuesta de compensación, almacena cierta cantidad de corriente en él.

Ahora, tan pronto como el mosfet se apaga, pasa al estado APAGADO bloqueando cualquier paso de la corriente de entrada.

Una vez más, el inductor no puede hacer frente a este cambio repentino de corriente de una magnitud dada a cero, y en una respuesta para compensar esto, retrocede su corriente almacenada a través del diodo a través de la salida del circuito.

En el proceso, la corriente también se almacena en el condensador.

Durante el siguiente estado ON del mosfet, el ciclo se repite como se indicó anteriormente, sin embargo, sin corriente disponible del inductor, el condensador descarga la energía almacenada en la salida, lo que ayuda a mantener la salida estable en el grado optimizado.

Puede que se pregunte qué factor decide los resultados BUCK o BOOST en la salida. Es bastante simple, depende de cuánto tiempo se le permite al mosfet permanecer en el estado ON o en el estado OFF.

Con un aumento en el tiempo de encendido de los mosfets, el circuito comienza a transformarse en un convertidor Boost mientras que con el tiempo de apagado de los mosfets que excede su tiempo de encendido, el circuito se comporta como un convertidor Buck.

Por lo tanto, la entrada al mosfet se puede realizar a través de un circuito PWM optimizado para obtener las transiciones requeridas en el mismo circuito.

Exploración más técnica de la topología Buck / Boost en circuitos SMPS:

Como se discutió en la sección anterior, las tres topologías fundamentales que se utilizan popularmente con las fuentes de alimentación conmutadas son el buck, boost y el buck boosts.

Estos son básicamente no aislados en los que la etapa de potencia de entrada comparte una base común con la sección de potencia de salida. Por supuesto también podríamos encontrar versiones aisladas aunque bastante raras.

Las tres topologías expresadas anteriormente se pueden distinguir de forma única dependiendo de sus propiedades exclusivas. Las propiedades pueden identificarse como las relaciones de conversión de voltaje de estado estable, la naturaleza de las corrientes de entrada y salida y el carácter de la ondulación del voltaje de salida también.

Además, la respuesta de frecuencia del ciclo de trabajo a la ejecución del voltaje de salida puede considerarse como una de las propiedades importantes.

Entre las tres topologías mencionadas anteriormente, la topología reductora-impulsora es la más preferida porque permite que la salida trabaje voltajes menores que la tensión de entrada (modo reductor) y también producir voltajes por encima de la tensión de entrada (modo impulso).

Sin embargo, la tensión de salida se puede adquirir siempre con la polaridad opuesta a la de la entrada, lo que no crea ningún problema.

La corriente de entrada aplicada a un convertidor reductor elevador es la forma de una corriente pulsante debido a la conmutación del interruptor de alimentación asociado (Q1).

Aquí, la corriente cambia de cero a 1 durante cada ciclo de pulso. Lo mismo ocurre con la salida también y obtenemos una corriente pulsante debido al diodo asociado que conduce solo en una dirección, lo que provoca una situación de pulsación ON y OFF durante el ciclo de conmutación. .

El condensador es responsable de proporcionar la corriente de compensación cuando el diodo está en el estado APAGADO o polarizado inverso durante los ciclos de conmutación.

Este artículo explica la funcionalidad de estado estable del convertidor reductor-elevador en modo continuo y funcionamiento en modo discontinuo con formas de onda ejemplares presentadas.

La funcionalidad de intercambio de voltaje de ciclo de trabajo a salida se presenta después de una introducción del diseño del interruptor PWM.

La figura 1 es un esquema simplista de la etapa de potencia reductor-elevador con un bloque de circuito de control agregado. El interruptor de encendido, Q1, es un MOSFET de canal n. El diodo de salida es CR1.

El inductor L y el condensador C constituyen el filtrado de salida eficiente. El condensador ESR, RC, (resistencia en serie equivalente) y la resistencia de CC del inductor, RL, se analizan en el. La resistencia, R, corresponde a la carga identificada por la salida de la etapa de potencia.

En el transcurso de la funcionalidad regular de la etapa de potencia reductora-elevadora, Q1 se enciende y apaga constantemente con los tiempos de encendido y apagado gobernados por el circuito de control.

Este comportamiento de conmutación permite una cadena de pulsos en la unión de Q1, CR1 y L.

Aunque el inductor, L, está vinculado al capacitor de salida, C, si solo CR1 conduce, se establece un filtro de salida L / C exitoso. Limpia la sucesión de pulsos para dar como resultado un voltaje de salida de CC.

Análisis de estado estable de la etapa Buck-Boost

Una etapa de potencia puede funcionar en un ajuste de corriente de inductor continuo o discontinuo. El modo de corriente continua del inductor se identifica por la corriente continua en el inductor sobre la secuencia de conmutación en el proceso de estado estable.

El modo de corriente del inductor discontinuo se identifica porque la corriente del inductor permanece cero durante una sección del ciclo de conmutación. Comienza en cero, se extiende hasta un valor máximo y vuelve a cero en el transcurso de cada patrón de conmutación.

Los dos métodos distintos se mencionan con mucho más detalle después y se presentan sugerencias de modelos para que el valor del inductor mantenga un modo seleccionado de funcionalidad como la capacidad de carga nominal. Es bastante favorable que un convertidor esté en un formato único solo en sus circunstancias de funcionamiento previstas, ya que la respuesta de frecuencia de la etapa de potencia se altera sustancialmente entre las dos técnicas distintas de funcionamiento.

Con esta evaluación, se emplea un MOSFET de potencia de canal n y el circuito de control suministra un voltaje positivo, VGS (ON), desde la puerta a los terminales de fuente de Q1 para encender el FET. El beneficio de emplear un FET de canal n es su RDS más bajo (encendido), sin embargo, el circuito de control es complicado porque se necesita una unidad suspendida. Para dimensiones idénticas del paquete, un FET de canal p posee un RDS (encendido) más alto, sin embargo, por lo general, puede que no necesite un circuito de control flotante.

El transistor Q1 y el diodo CR1 se ilustran dentro de un contorno de línea discontinua con terminales etiquetados como a, py c. Se trata a fondo en la sección Modelado de etapas de potencia de Buck-Boost.

Análisis del modo de conducción continua en estado estacionario Buck-Boost

La siguiente es una descripción del funcionamiento del impulso reductor en la operación de estado estable en el método de conducción continua. El objetivo principal de este segmento sería presentar una derivación de la relación de transformación de voltaje para la etapa de potencia buck-boost en modo de conducción continua.

Esto será significativo ya que indica la forma en que el voltaje de salida está determinado por el ciclo de trabajo y el voltaje de entrada o, por el contrario, cómo se puede determinar el ciclo de trabajo según el voltaje de entrada y el voltaje de salida.

Estado estable significa que el voltaje de entrada, el voltaje de salida, la corriente de carga de salida y el ciclo de trabajo son constantes en lugar de variar. Por lo general, se proporcionan letras mayúsculas a las etiquetas de variables para sugerir una magnitud de estado estable. En el modo de conducción continua, el convertidor reductor-elevador toma un par de estados por ciclo de conmutación.

El estado ON es cada vez que Q1 está ON y CR1 está OFF. El estado APAGADO es cada vez que Q1 está APAGADO y CR1 está ENCENDIDO. Un circuito lineal sencillo podría simbolizar cada uno de los dos estados en los que los interruptores del circuito se sustituyen por su circuito de adaptación en el curso de cada estado. El diagrama de circuito para cada una de las dos condiciones se presenta en la Figura 2.

El período de la condición ON es D × TS = TON en el que D es el ciclo de trabajo, fijado por el circuito de excitación, representado en forma de una relación entre el período de conmutación ON y el período de una única secuencia de conmutación completa, Ts.

La duración del estado OFF se conoce como TOFF. Debido a que se pueden encontrar solo un par de condiciones por ciclo de conmutación para el modo de conducción continua, TOFF es igual a (1 − D) × TS. La magnitud (1 − D) se denomina ocasionalmente D '. Estos períodos se presentan junto con las formas de onda en la Figura 3.

Mirando la Figura 2, en el curso del estado ON, Q1 ofrece una resistencia reducida, RDS (encendido), desde su drenaje hasta la fuente y manifiesta una caída de voltaje menor de VDS = IL × RDS (encendido).

Además, hay una pequeña caída de voltaje en la resistencia de CC del inductor igual a IL × RL.

Por lo tanto, el voltaje de entrada, VI, menos los déficits, (VDS + IL × RL), se activa a través del inductor, L. CR1 está APAGADO dentro de este período, ya que tendría polarización inversa.

La corriente del inductor, IL, pasa de la fuente de entrada, VI, a través de Q1 y a tierra. En el curso del estado ON, la tensión aplicada a través del inductor es constante y es la misma que VI - VDS - IL × RL.

Siguiendo la norma de polaridad para la corriente IL presentada en la Figura 2, la corriente del inductor aumenta debido al voltaje ejecutado. Además, debido a que el voltaje aplicado es fundamentalmente consistente, la corriente del inductor aumenta linealmente. Este aumento en la corriente del inductor en el curso de TON se muestra en la Figura 3.

El nivel por el cual aumenta la corriente del inductor generalmente se determina utilizando una forma de la fórmula conocida:

El aumento de la corriente del inductor en el curso del estado ON se presenta como:

Esta magnitud, ΔIL (+), se denomina corriente de ondulación del inductor. Además, observe que a través de este intervalo, cada bit de la corriente de carga de salida entra por el capacitor de salida, C.

Con referencia a la Figura 2, mientras Q1 está APAGADO, ofrece una mayor impedancia desde su drenaje a la fuente.

En consecuencia, debido a que la corriente que circula en el inductor L no puede ajustarse instantáneamente, la corriente cambia de Q1 a CR1. Como resultado de la reducción de la corriente del inductor, el voltaje a través del inductor invierte la polaridad hasta que el rectificador CR1 se convierte en polarización directa y se enciende.

El voltaje conectado a través de L se convierte en (VO - Vd - IL × RL) en el que la magnitud, Vd, es la caída de voltaje directo de CR1. La corriente del inductor, IL, en este punto pasa desde el condensador de salida y la disposición de la resistencia de carga a través de CR1 y a la línea negativa.

Observe que la alineación de CR1 y la ruta de circulación de la corriente en el inductor significa que la corriente que corre en el condensador de salida y la agrupación de resistencias de carga conduce a que VO sea un voltaje negativo. En el curso del estado APAGADO, el voltaje conectado a través del inductor es estable y es el mismo que (VO - Vd - IL × RL).

Preservando nuestra convención de polaridad similar, este voltaje conectado es menos (o invierte la polaridad del voltaje conectado en el transcurso del tiempo de ENCENDIDO), debido al hecho de que el voltaje de salida VO es negativo.

Por lo tanto, la corriente del inductor disminuye durante el tiempo de APAGADO. Además, debido a que el voltaje conectado es básicamente estable, la corriente del inductor se reduce linealmente. Esta reducción en la corriente del inductor en el curso de TOFF se describe en la Figura 3.

La reducción de la corriente del inductor a través de la situación OFF es proporcionada por:

Esta magnitud, ΔIL (-), puede denominarse corriente de ondulación del inductor. En situaciones de estado estable, el aumento de corriente, ΔIL (+), en el transcurso del tiempo ON y la reducción de corriente a través del tiempo OFF, ΔIL (-), tiene que ser idéntico.

De lo contrario, la corriente del inductor podría ofrecer un impulso o reducción general de un ciclo a otro que no sería una circunstancia de condición estable.

Por lo tanto, ambas ecuaciones pueden equipararse y elaborarse para que VO adquiera la forma de conducción continua de afiliación de cambio de voltaje reductor-elevador:

Determinación de VO:

Además, sustituyendo TS por TON + TOFF y empleando D = TON / TS y (1 − D) = TOFF / TS, la ecuación de estado estable para VO es:

Observe que al simplificar lo anterior, se supone que TON + TOFF es similar a TS. Esto puede ser genuino solo para el modo de conducción continua como vamos a descubrir en la evaluación del modo de conducción discontinua. En este punto debe hacerse un escrutinio esencial:

Fijar los dos valores de ΔIL a la par entre sí es exactamente igual a nivelar los voltios-segundos en el inductor. Los voltios-segundos empleados en el inductor son el producto del voltaje empleado y el período durante el cual se aplica el voltaje.

Esta puede ser la forma más eficaz de estimar magnitudes no identificadas, por ejemplo, VO o D con respecto a parámetros de circuito comunes, y este enfoque se utilizará con frecuencia en este artículo. La estabilización de voltios por segundo en el inductor es un requisito natural y debe percibirse, al menos además, como la ley de Ohm.

En las ecuaciones anteriores para ΔIL (+) y ΔIL (-), se suponía implícitamente que el voltaje de salida era consistente sin ningún voltaje de ondulación de CA durante el tiempo de ENCENDIDO y el período de APAGADO.

Ésta es una simplificación aceptada e implica un par de resultados individuales. En primer lugar, se cree que el condensador de salida tiene un tamaño adecuado y que su conversión de voltaje es mínima.

En segundo lugar, el voltaje del condensador ESR además se considera mínimo. Tales suposiciones son legítimas ya que el voltaje de rizado de CA definitivamente será significativamente menor que la porción de CC del voltaje de salida.

La alteración de voltaje anterior para VO demuestra la verdad de que el VO podría ajustarse ajustando el ciclo de trabajo, D.

Esta conexión se acerca a cero cuando D llega cerca de cero y aumenta sin destino cuando D se acerca a 1. Una simplificación típica considera que VDS, Vd y RL son lo suficientemente pequeños como para descuidarlos. Al establecer VDS, Vd y RL a cero, la fórmula anterior se simplifica notablemente a:

Un método cualitativo menos complicado para imaginar el funcionamiento del circuito sería considerar el inductor como una parte de almacenamiento de energía. Cada vez que Q1 está encendido, se vierte energía sobre el inductor.

Mientras Q1 está apagado, el inductor devuelve parte de su energía al condensador de salida y a la carga. El voltaje de salida se regula estableciendo el tiempo de activación de Q1. Por ejemplo, al aumentar el tiempo de activación de Q1, se amplifica la cantidad de energía enviada al inductor.

Posteriormente, se envía energía adicional a la salida durante el tiempo de inactividad de Q1, lo que provoca un aumento en la tensión de salida. En contraste con la etapa de potencia reductora, la magnitud típica de la corriente del inductor no es la misma que la corriente de salida.

Para asociar la corriente del inductor a la corriente de salida, observando las Figuras 2 y 3, observe que la corriente del inductor a la salida está únicamente en el estado apagado de la etapa de potencia.

Esta corriente promediada en toda una secuencia de conmutación es la misma que la corriente de salida, ya que la corriente aproximada en el condensador de salida debería ser equivalente a cero.

La conexión entre la corriente media del inductor y la corriente de salida para la etapa de potencia reductor-reforzador de modo continuo es proporcionada por:

Otro punto de vista significativo es el hecho de que la corriente típica del inductor es proporcional a la corriente de salida, y debido a que la corriente de ondulación del inductor, ΔIL, no está relacionada con la corriente de carga de salida, los valores mínimo y más alto de la corriente del inductor siguen la corriente promedio del inductor con precisión.

Como ejemplo, si la corriente promedio del inductor disminuye en 2A debido a una reducción de la corriente de carga, en ese caso los valores más bajos y más altos de la corriente del inductor se reducen en 2A (considerando que se conserva el modo de conducción continua).

La evaluación anterior fue para la funcionalidad de la etapa de potencia reductor-elevador en modo de corriente de inductor continuo. El siguiente segmento es una explicación de la funcionalidad de estado estable en modo de conducción discontinua. El resultado principal es una derivación de la relación de conversión de voltaje para la etapa de potencia reductor-reforzador del modo de conducción discontinua.

Evaluación del modo de conducción discontinua en estado estacionario Buck-Boost

En este punto, examinamos qué ocurre cuando se reduce la corriente de carga y el modo de conducción cambia de continuo a discontinuo.

Recuerde que para el modo de conducción continua, la corriente promedio del inductor sigue la corriente de salida, es decir, en caso de que la corriente de salida se reduzca, en ese caso también lo hará la corriente promedio del inductor.

Además, los picos más bajos y más altos de la corriente del inductor persiguen con precisión la corriente promedio del inductor. En caso de que la corriente de carga de salida disminuya por debajo del nivel de corriente fundamental, la corriente del inductor sería cero para una parte de la secuencia de conmutación.

Esto sería evidente a partir de las formas de onda presentadas en la Figura 3, porque el nivel de pico a pico de la corriente de ondulación no se puede alterar con la corriente de carga de salida.

En una etapa de potencia reductora-elevadora, si la corriente del inductor intenta bajar de cero, simplemente se detiene en cero (debido al movimiento de corriente unidireccional en CR1) y continúa allí hasta el comienzo de la acción de conmutación subsiguiente. Este modo de trabajo se conoce como modo de conducción discontinua.

Un funcionamiento de etapa de potencia del circuito reductor elevador en formato de conducción discontinua posee tres estados distintivos a través de cada ciclo de conmutación en contraste con 2 estados para el formato de conducción continua.

El estado de corriente del inductor en el que la etapa de potencia se encuentra en la periferia entre el ajuste continuo y discontinuo se presenta en la Figura 4.

En esto, la corriente del inductor simplemente colapsa a cero, mientras que el siguiente ciclo de conmutación comienza justo después de que la corriente llega a cero. Observe que los valores de IO e IO (Crit) se muestran en la Figura 4 ya que IO e IL incluyen polaridades opuestas.

Una mayor reducción de la corriente de carga de salida establece la etapa de potencia en un patrón de conducción discontinua. Esta condición se dibuja en la Figura 5.

La respuesta de frecuencia de la etapa de potencia de modo discontinuo es bastante diferente de la respuesta de frecuencia de modo continuo que se presenta en el segmento de modelado de etapa de potencia Buck-Boost. Además, la conexión de entrada a salida es bastante diversa como se presenta en la derivación de esta página:

Para iniciar la derivación de la relación de cambio de voltaje de la etapa de potencia reductor-impulso del modo de conducción discontinua, recuerde que tiene tres estados distintivos que el convertidor considera a través de la funcionalidad del modo de conducción discontinua.

El estado ON es cuando Q1 está ON y CR1 está OFF. El estado APAGADO es cuando Q1 está APAGADO y CR1 está ENCENDIDO. La condición IDLE es cuando cada Q1 y CR1 están APAGADOS. Las dos condiciones iniciales son muy parecidas a la situación del modo continuo y los circuitos de la Figura 2 son relevantes aparte de TOFF ≠ (1 − D) × TS. El resto de la secuencia de conmutación es el estado INACTIVO.

Además, la resistencia de CC del inductor de salida, la caída de voltaje directo del diodo de salida, así como la caída de voltaje del estado ON del MOSFET de potencia, generalmente se supone que son lo suficientemente pequeñas como para pasarlas por alto.

El período de tiempo del estado ON es TON = D × TS donde D es el ciclo de trabajo, fijado por el circuito de control, indicado como una relación entre el tiempo de encendido y el tiempo de una secuencia de conmutación completa, Ts. La longitud del estado APAGADO es TOFF = D2 × TS. El período IDLE es el resto del patrón de conmutación que se presenta como TS - TON - TOFF = D3 × TS. Estos períodos se soportan con las formas de onda de la Figura 6.

Sin verificar la descripción completa, las ecuaciones para el aumento y la caída de la corriente del inductor se enumeran a continuación. El aumento de la corriente del inductor en el curso del estado ON es emitido por:

La cantidad de corriente de ondulación, ΔIL (+), es igualmente la corriente de pico del inductor, Ipk, ya que en el modo discontinuo, la corriente comienza en 0 en cada ciclo.

Al igual que en la situación del modo de conducción continua, el aumento de corriente, ΔIL (+), en el transcurso del tiempo ON y la reducción de corriente mientras está en el tiempo OFF, ΔIL (-), son idénticas. Por lo tanto, ambas ecuaciones podrían equipararse y abordarse para que VO adquiera la inicial de dos ecuaciones que se utilizarán para resolver la relación de conversión de voltaje:

A continuación, determinamos la corriente de salida (el voltaje de salida VO dividido por la carga de salida R). Es el promedio de una secuencia de conmutación de la corriente del inductor en el momento en que CR1 se vuelve conductor (D2 × TS).

Aquí, reemplace la conexión para IPK (ΔIL (+)) en la ecuación anterior para adquirir:

Por lo tanto, tenemos dos ecuaciones, la de la corriente de salida (VO dividido por R) recién derivada y la de la tensión de salida, ambas con respecto a VI, D y D2. En este punto, desentrañamos cada fórmula para D2 y arreglamos las dos ecuaciones a la par.

Utilizando la ecuación resultante, podría obtenerse una ilustración para el voltaje de salida, VO. La afiliación de transformación de voltaje reductor-elevador del modo de conducción discontinua está escrita por:

La conexión anterior muestra una de las principales diferencias entre los dos modos de conducción. Para el modo de conducción discontinua, la relación de cambio de voltaje es una función del voltaje de entrada, ciclo de trabajo, inductancia de la etapa de potencia, frecuencia de conmutación y resistencia de carga de salida.

Para el modo de conducción continua, la conexión de cambio de voltaje solo está influenciada por el voltaje de entrada y el ciclo de trabajo. En aplicaciones tradicionales, la etapa de potencia reductora-elevadora se ejecuta en una opción entre el modo de conducción continua o el modo de conducción discontinua. Para un uso específico, se elige un modo de conducción mientras que la etapa de potencia se hizo para sostener el modo idéntico.