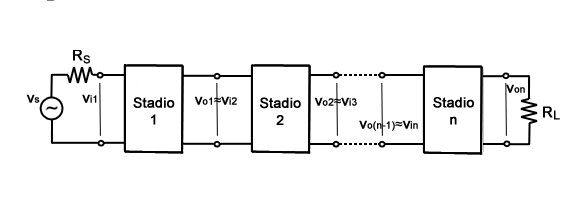
Un filtro se puede definir como un tipo de circuito utilizado para remodelar, modificar y rechazar todas las frecuencias no deseadas de una señal. Un filtro RC ideal dividirá y permitirá el paso de señales de entrada (sinusoidales) dependiendo de la frecuencia. Generalmente, en baja frecuencia (<100 kHz) applications, passive filtros se construyen utilizando componentes de resistencia y condensador. Por eso se conoce como filtro RC pasivo . De manera similar, para señales de alta frecuencia (> 100 kHz), los filtros pasivos se pueden diseñar con componentes resistor-inductor-capacitor. Entonces estos circuitos se denominan pasivos Circuitos RLC . Estos filtros se denominan así en función del rango de frecuencia de la señal que dejan pasar. Normalmente se utilizan tres diseños de filtro, como filtro de paso bajo, filtro de paso alto , y filtro de paso de banda . Este artículo analiza una descripción general del filtro de paso bajo.
¿Qué es un filtro de paso bajo?
los definición de filtro de paso bajo o LPF es un tipo de filtro que se utiliza para pasar señales con baja frecuencia y también para atenuar con alta frecuencia que una frecuencia de corte preferida. los respuesta de frecuencia del filtro de paso bajo depende principalmente de la Paso bajo diseño de filtro . Estos filtros existen en varias formas y dan el tipo más suave de señal. Los diseñadores utilizarán frecuentemente estos filtros como un filtro prototipo con impedancia y ancho de banda unitario.
El filtro preferido se obtiene de la muestra equilibrando la impedancia y el ancho de banda preferidos, y cambia al tipo de banda preferido como paso bajo (LPF), paso alto (HPF) , paso de banda (BPSF) o parada de banda (BSF).
Filtro de paso bajo de primer orden
En la figura se muestra un LPF de primer orden. ¿Qué es este circuito? Un integrador simple. Tenga en cuenta que el integrador es el bloque de construcción básico para LPF.

Filtro de paso bajo de primer orden
Asumir Z1 = 1 / 𝑗⍵𝐶1
V1 = Vi * 𝑍1 / 𝑅1 + 𝑍1 = Vi (1 / 𝑗⍵𝐶1) / 𝑅1 + (1 / 𝑗⍵𝐶1)
= Vi 1 / 𝑗𝜔𝐶1𝑅1 + 1
= Vi 1 / 𝑠𝐶1𝑅1 + 1
Aquí s = j⍵
función de transferencia de filtro de paso bajo es
𝑉1 / 𝑉𝑖 = 1 / 𝑠𝐶1𝑅1 + 1
La salida se reduce (atenúa) inversamente a la frecuencia. Si la frecuencia se duplica, la salida es la mitad (-6 dB por cada duplicación de frecuencia, de lo contrario, - 6 dB por octava). Este es un LPF de primer orden y la atenuación es de -6 dB por octava.
Filtro de paso bajo de segundo orden
los filtro de paso bajo de segundo orden se muestra en la figura.

Filtro de paso bajo de segundo orden
Asumir Z1 = 1 / 𝑗⍵𝐶1
V1 = Vi 𝑍1 / 𝑅1 + 𝑍1
Vi * (1 / 𝑗⍵𝐶1) / 𝑅1 + (1 / 𝑗⍵𝐶1)
Vi 1 / 𝑗𝜔𝐶1𝑅1 + 1
= Vi 1 / 𝑠𝐶1𝑅1 + 1
Aquí s = j⍵
Función de transferencia de filtro de paso bajo
𝑉1 / 𝑉𝑖 = 1 / 𝑠𝐶1𝑅1 + 1
Asumir Z2 = 1 / 𝑗⍵𝐶1
V1 = Vi 𝑍2 / 𝑅2 + 𝑍2
Vi * (1 / 𝑗⍵𝐶2) / 𝑅2 + (1 / 𝑗⍵𝐶2)
Vi 1 / 𝑗𝜔𝐶2𝑅2 + 1
= Vi 1 / 𝑠𝐶2𝑅2 + 1
Vi (1 / 𝑠𝐶1𝑅1 + 1) * (1 / 𝑠𝐶2𝑅2 + 1)
= 1 / (𝑠2𝑅1𝑅2𝐶1𝐶2 + 𝑠 (𝑅1𝐶1 + 𝑅2𝐶2) +1)
Por tanto, la función de transferencia es una ecuación de segundo orden.
𝑉𝑜 / 𝑉𝑖 = 1 / (𝑠2𝑅1𝑅2𝐶1𝐶2 + 𝑠 (𝑅1𝐶1 + 𝑅2𝐶2) +1)
La salida se reduce (atenúa) inversamente al cuadrado de la frecuencia. Si la frecuencia duplica la salida es c1 / 4th. (- 12 dB por cada duplicación de frecuencia o - 12 dB por octava). Este es un filtro de paso bajo de segundo orden y el balanceo es de -12 dB por octava.
los filtro de paso bajo diagrama de bode se muestra a continuación. En general, la respuesta de frecuencia de un filtro de paso bajo se indica con la ayuda de un diagrama de Bode, y este filtro se distingue por su frecuencia de corte y por la tasa de caída de frecuencia.
Filtro de paso bajo con amplificador operacional
Amplificadores operacionales o amplificadores operacionales suministra filtros de paso bajo muy eficientes sin utilizar inductores. El circuito de retroalimentación de un amplificador operacional se puede incorporar con los elementos básicos de un filtro, por lo que los LPF de alto rendimiento se forman fácilmente utilizando los componentes necesarios, excepto los inductores. los aplicaciones de amplificador operacional Los LPF se utilizan en diferentes áreas de fuentes de alimentación a las salidas de DAC (convertidores digitales a analógicos) para eliminar señales de alias y otras aplicaciones.
Circuito LPF activo de primer orden con amplificador operacional
los diagrama de circuito del unipolar o de primer orden filtro de paso bajo activo se muestra a continuación. El circuito de la filtro de paso bajo usando amplificador operacional usos un condensador a través de la resistencia de retroalimentación. Este circuito tiene un efecto cuando la frecuencia aumenta para mejorar el nivel de retroalimentación, luego cae la impedancia reactiva del capacitor.

Filtro de paso bajo de primer orden con amplificador operacional
El cálculo de este filtro se puede hacer trabajando en la frecuencia a la que la reactancia del capacitor puede igualar la resistencia de la resistencia. Esto se puede obtener usando la siguiente fórmula.
Xc = 1 / π f C
Donde 'Xc' es la reactancia capacitiva en ohmios
'Π' es la letra estándar y el valor de esta es 3.412
'F' es la frecuencia (Unidades-Hz)
'C' es la capacitancia (Unidades-Faradios)
La ganancia en banda de estos circuitos se puede calcular de forma sencilla eliminando el efecto del condensador.
Como estos tipos de circuitos son útiles para dar una reducción dentro de la ganancia a altas frecuencias, además de ofrecer una velocidad máxima de caída de 6 dB por cada octava, lo que significa que el voltaje o / p se divide para cada repetición en frecuencia. Por lo tanto, este tipo de filtro se denomina filtro de paso bajo de primer orden o unipolar.
Circuito LPF activo de segundo orden con amplificador operacional
Usando un amplificador operacional , es posible diseñar filtros en una amplia gama con niveles de ganancia diferentes, así como modelos de atenuación. Este filtro ofrece una respuesta de ancho de banda y una ganancia unitaria.

Circuito LPF activo de segundo orden con amplificador operacional
Los cálculos de los valores del circuito son sencillos para la respuesta de Filtro de paso bajo Butterworth y ganancia unitaria. Se necesita una amortiguación significativa para estos circuitos y los valores de relación del condensador y la resistencia concluyen esto.
R1 = R2
C1 = C2
f = 1 - √4 π R C2
Al seleccionar los valores, asegúrese de que los valores de la resistencia caigan en la región entre 10 kilos ohmios y 100 kiloohmios. Esto vale la pena ya que la impedancia o / p del circuito aumenta en la frecuencia y los valores externos de esta sección pueden cambiar el acto.
Calculadora de filtro de paso bajo
Para un RC circuito de filtro de paso bajo , la calculadora de filtro de paso bajo calcula la frecuencia de cruce y traza la Gráfico de filtro de paso bajo que se conoce como una parcela de bode.
Por ejemplo:
La función de transferencia del filtro de paso bajo se puede calcular utilizando la siguiente fórmula si conocemos los valores de la resistencia y el condensador en el circuito.
Vout (s) / Vin (s) + 1 / CR / s + 1 / CR
Calcule el valor de frecuencia para la resistencia dada, así como los valores del condensador.
fc = 1/2 πRC

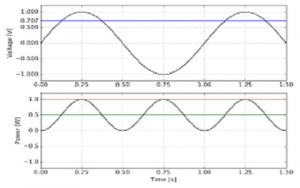
Forma de onda LPF
Aplicaciones de filtro de paso bajo
Las aplicaciones del filtro de paso bajo incluyen las siguientes.
- Los filtros de paso bajo se utilizan en sistemas telefónicos para convertir las frecuencias de audio en el altavoz en una señal de banda de voz limitada.
- Los LPF se utilizan para filtrar la señal de alta frecuencia que se conoce como 'ruido' de un circuito, ya que la señal pasa a través de este filtro, luego se elimina la mayor parte de la señal de alta frecuencia y se puede producir un ruido obvio.
- Filtro de paso bajo en procesamiento de imágenes para mejorar la imagen
- A veces, estos filtros se conocen como corte de agudos o corte de agudos debido a las aplicaciones en audio.
- Un filtro de paso bajo se utiliza en un circuito RC que se conoce como Filtro de paso bajo RC .
- LPF se utiliza como integrador como un circuito RC
- En DSP de velocidad múltiple, mientras se ejecuta un interpolador, LPF se utiliza como filtro anti-imágenes. Del mismo modo, al ejecutar un decimador, este filtro se utiliza como filtro anti-aliasing.
- Los filtros de paso bajo se utilizan en receptores como superheterodinos para una respuesta eficiente de las señales de banda base.
- El filtro de paso bajo se usa en las señales de dispositivos médicos que provienen del cuerpo humano, mientras que las pruebas con electrodos tienen menos frecuencia. Entonces, estas señales pueden fluir a través del LPF para eliminar algunos sonidos ambientales no deseados.
- Estos filtros se utilizan en la conversión de la amplitud del ciclo de trabajo, así como en la detección de fase en el bucle de bloqueo de fase.
- LPF se utiliza en radio AM para que el detector de diodos cambie la señal de frecuencia intermedia modulada AM a la señal de audio.
Por lo tanto, se trata de un filtro de paso bajo . El diseño de LPF basado en amplificador operacional es simple de diseñar, así como diseños más complicados que utilizan diferentes tipos de filtros. Para más aplicaciones, el LPF proporciona un rendimiento excepcional. Aquí hay una pregunta para usted, ¿cuál es la función principal del filtro de paso bajo?