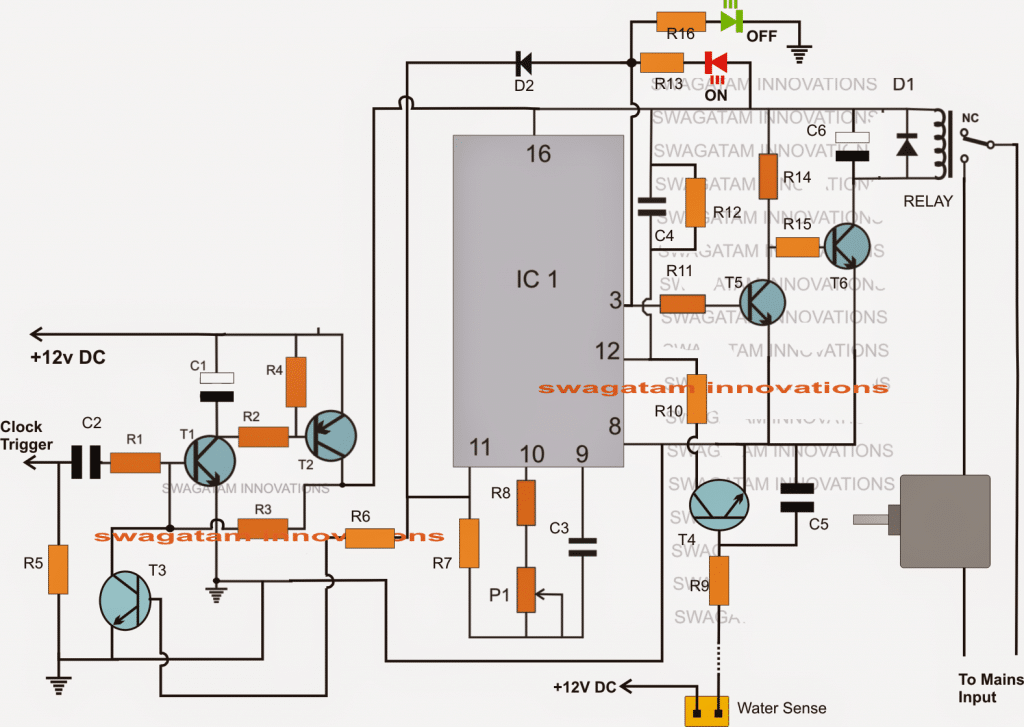
En este artículo intentamos comprender la ley de Ohm y la ley de Kirchhoff a través de fórmulas y explicaciones de ingeniería estándar, y aplicando ecuaciones diferenciales lineales de primer orden para resolver conjuntos de problemas de ejemplo.
¿Qué es un circuito eléctrico?
Un circuito eléctrico más simple generalmente tiene la forma de un circuito en serie que tiene una fuente de energía o una entrada de fuerza electromotriz, como una batería o un generador de CC, y una carga resistiva que consume esta energía, por ejemplo, una bombilla eléctrica, como se muestra en el diagrama de abajo:

Refiriéndose al diagrama, cuando el interruptor está cerrado, la corriente I pasa a través de la resistencia, lo que hace que se genere un voltaje a través de la resistencia. Es decir, cuando se miden, las diferencias de potencial en los dos puntos finales de la resistencia mostrarán valores diferentes. Esto se puede confirmar con un voltímetro.
De la situación explicada anteriormente, la ley de Ohm estándar se puede deducir como:
La caída de voltaje ER a través de una resistencia es proporcional a la corriente instantánea I, y puede expresarse como:
ER = RI (Ecuación # 1)
En la expresión anterior, R se define como la constante de proporcionalidad y se llama resistencia del resistor.
Aquí medimos el voltaje ES en voltios, la resistencia R en ohmios, y la corriente I en amperios.
Esto explica la ley de Ohm en su forma más básica dentro de un circuito eléctrico simple.
En circuitos más complejos, se incluyen dos elementos esenciales más en forma de condensadores e inductores.
¿Qué es un inductor?
Un inductor puede definirse como un elemento que se opone a un cambio en la corriente, creando un efecto similar a la inercia en el flujo de electricidad, al igual que lo hace una masa en los sistemas mecánicos. Los experimentos han producido lo siguiente para inductores:
La caída de voltaje EL a través de un inductor es proporcional a la tasa de cambio de tiempo instantáneo de la corriente I. Esto se puede expresar como:
EL = L dl / dt (Ecuación # 2)
donde L se convierte en la constante de proporcionalidad y se denomina inductancia del inductor, y se mide en henrys. El tiempo t se expresa en segundos.
¿Qué es un condensador?
Un condensador es simplemente un dispositivo que almacena energía eléctrica. Los experimentos nos permiten obtener la siguiente explicación:
La caída de voltaje a través de un capacitor es proporcional a la carga eléctrica instantánea Q en el capacitor, esto puede expresarse como:
EC = 1 / C x Q (Ecuación # 3)
donde C se denomina como capacidad , y se mide en faradios la carga Q se mide en culombios.
sin embargo, desde Yo (c) = dQ / dt, podemos escribir la ecuación anterior como:

El valor de la corriente Eso) se puede resolver en un circuito dado resolviendo la ecuación producida por la aplicación de la siguiente ley física:
Comprensión de la ley de Kirchhoff (KVL)
Gustav Robert Kirchhoff (1824-1887) fue un físico alemán, sus leyes populares pueden entenderse como se narran a continuación:
La ley actual de Kirchhoff (KCL) establece que:
En cualquier punto de un circuito, la suma de las corrientes de entrada es igual a la suma de la corriente de salida.
La ley de voltaje de Kirchhoff (KVL) establece que:
La suma algebraica de todas las caídas de voltaje instantáneas alrededor de cualquier circuito cerrado es cero, o el voltaje impreso en un circuito cerrado es igual a la suma de las caídas de voltaje en el resto del circuito.
Ejemplo 1: Con referencia al diagrama RL a continuación, y combinando la Ecuación # 1,2 y el voltaje de Kirchhoff, podemos derivar la siguiente expresión:

Ecuación: 4
Consideremos este caso A con una fuerza electromotriz constante:

En la ecuación # 4 descrita anteriormente, si E = E0 = constante, entonces podemos generar la siguiente ecuación:

Ecuación: 5
Aquí el último término se acerca a cero cuando t tiende a proceder al infinito, de modo que Eso) tiende al valor límite E0 / R. Tras un retraso suficientemente largo, llegaré a una prácticamente constante, sin depender del valor de c, lo que también implica que esta será independiente de una condición inicial que podamos forzar.
Considerando que la condición inicial es I (0) = 0, obtenemos:
 Ecuación: 5 *
Ecuación: 5 *
Caso B (Fuerza electromotriz periódica):

Considerando E (t) = Eo sen ωt, luego, teniendo en cuenta la Ecuación # 4, la solución general para el Caso B se puede escribir como:
 (∝ = R / L)
(∝ = R / L)
Integrarlo por partes nos da:

Esto se puede derivar además como:
 ઠ = arco hasta ωL / R
ઠ = arco hasta ωL / R
Aquí, el término exponencial tiende a acercarse a cero ya que t tiende a llegar al infinito. Esto implica que una vez transcurrido un período de tiempo suficientemente largo, la corriente I (t) alcanza oscilaciones prácticamente armónicas.
Anterior: ¿Qué es la saturación de transistores? Siguiente: Análisis de línea de carga en circuitos BJT