En esta publicación, intentaremos comprender los diversos parámetros necesarios para diseñar un inductor de convertidor reductor correcto, de modo que la salida requerida sea capaz de lograr la máxima eficiencia.
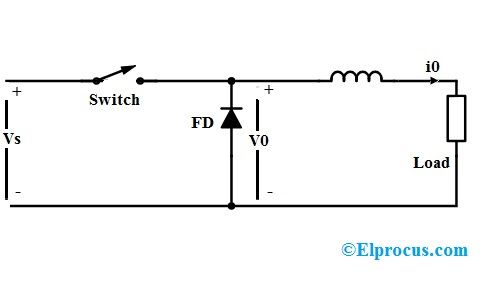
En nuestro post anterior aprendimos el conceptos básicos de convertidores buck y se dio cuenta del aspecto importante con respecto al tiempo de ENCENDIDO del transistor con respecto al tiempo periódico del PWM que esencialmente determina el voltaje de salida del convertidor reductor.
En esta publicación, profundizaremos un poco más y trataremos de evaluar la relación entre el voltaje de entrada, el tiempo de conmutación del transistor, el voltaje de salida y la corriente del inductor reductor, y con respecto a cómo optimizarlos al diseñar un inductor reductor.

Especificaciones del convertidor Buck
Primero entendamos los diversos parámetros involucrados con un convertidor de dólar:
Corriente máxima del inductor, ( Ipaquete ) = Es la cantidad máxima de corriente que puede almacenar un inductor antes de saturarse. Aquí, el término 'saturado' significa una situación en la que el tiempo de conmutación del transistor es tan largo que continúa encendido incluso después de que el inductor haya cruzado su capacidad máxima o máxima de almacenamiento de corriente. Esta es una situación indeseable y debe evitarse.
Corriente mínima del inductor, ( Io ) = Es la cantidad mínima de corriente que puede permitirse que alcance el inductor mientras el inductor se descarga liberando su energía almacenada en forma de EMF inverso.
Es decir, en el proceso cuando el transistor se apaga, el inductor descarga su energía almacenada a la carga y en el curso su corriente almacenada cae exponencialmente hacia cero, sin embargo, antes de llegar a cero, se puede suponer que el transistor se enciende nuevamente, y esto El punto en el que el transistor puede volver a encenderse se denomina corriente mínima del inductor.
La condición anterior también se denomina modo continuo para un diseño de convertidor de dólar .
Si el transistor no se enciende antes de que la corriente del inductor haya caído a cero, entonces la situación puede denominarse modo discontinuo, que es una forma indeseable de operar un convertidor reductor y puede conducir a un funcionamiento ineficiente del sistema.
Corriente de ondulación, (Δi = Ipaquete - Io ) = Como puede verse en la fórmula adjunta, la ondulación Δ i es la diferencia entre la corriente máxima y la corriente mínima inducida en el inductor reductor.
Un condensador de filtro en la salida del convertidor reductor normalmente estabilizará esta corriente de ondulación y ayudará a que sea relativamente constante.
Ciclo de trabajo, (D = Ten / T) = El ciclo de trabajo se calcula dividiendo el tiempo de ENCENDIDO del transistor por el tiempo periódico.
El tiempo periódico es el tiempo total que tarda un ciclo de PWM en completarse, es decir, el tiempo de ENCENDIDO + el tiempo de APAGADO de un PWM alimentado al transistor.
ON tiempo del transistor ( Ten = D / f) = El tiempo de ENCENDIDO del PWM o el tiempo de 'encendido' del transistor se puede lograr dividiendo el ciclo de trabajo por la frecuencia.
Corriente de salida promedio o corriente de carga, ( Iave = Δi / 2 = i carga ) = Se obtiene dividiendo la corriente de ondulación por 2. Este valor es el promedio de la corriente máxima y la corriente mínima que puede estar disponible a través de la carga de una salida de convertidor reductor.
Valor RMS de la onda triangular irms = √ { Io 2 + (Δi) 2 / 12} = Esta expresión nos proporciona el RMS o el valor cuadrático medio de todos o cualquier componente de onda triangular que puede estar asociado con un convertidor reductor.
Bien, entonces los anteriores fueron los diversos parámetros y expresiones esencialmente involucrados con un convertidor reductor que se podría utilizar al calcular un inductor reductor.
Ahora aprendamos cómo el voltaje y la corriente pueden estar relacionados con un inductor reductor y cómo se pueden determinar correctamente, a partir de los siguientes datos explicados:
Recuerde que aquí asumimos que la conmutación del transistor está en modo continuo, es decir, el transistor siempre se enciende antes de que el inductor pueda descargar su EMF almacenado por completo y se vacíe.
En realidad, esto se hace dimensionando adecuadamente el tiempo de ENCENDIDO del transistor o el ciclo de trabajo PWM con respecto a la capacidad del inductor (número de vueltas).
Relación V e I
La relación entre voltaje y corriente dentro de un inductor reductor se puede establecer como:
V = L di / dt
o
i = 1 / L 0ʃtVdt + io
La fórmula anterior puede usarse para calcular la corriente de salida reductora y es válida cuando el PWM tiene la forma de una onda que sube y baja exponencialmente, o puede ser una onda triangular.
Sin embargo, si el PWM tiene forma de onda rectangular o pulsos, la fórmula anterior se puede escribir como:
yo = (Vt / L) + yoo
Aquí Vt es el voltaje a través del devanado multiplicado por el tiempo durante el cual se mantiene (en microsegundos)
Esta fórmula se vuelve importante al calcular el valor de inductancia L para un inductor reductor.
La expresión anterior revela que la salida de corriente de un inductor reductor tiene la forma de una rampa lineal u ondas triangulares anchas, cuando el PWM tiene la forma de ondas triangulares.
Ahora veamos cómo se puede determinar la corriente máxima dentro de un inductor buck, la fórmula para esto es:
ipk = (Vin - Vtrans - Vout) Tonelada / L + io
La expresión anterior nos proporciona la corriente máxima mientras el transistor está encendido y la corriente dentro del inductor se acumula linealmente (dentro de su rango de saturación *)
Cálculo de la corriente máxima
Por lo tanto, la expresión anterior se puede usar para calcular la acumulación de corriente máxima dentro de un inductor reductor mientras el transistor está en la fase de encendido.
Si la expresión io se cambia a LHS obtenemos:
Ipaquete- Io= (Vino - Vtrans - Vout) Ton / L
Aquí Vtrans se refiere a la caída de voltaje en el colector / emisor del transistor
Recuerde que la corriente de ondulación también está dada por Δi = ipk - io, por lo tanto, sustituyendo esto en la fórmula anterior obtenemos:
Δi = (Vin - Vtrans - Vout) Ton / L ------------------------------------- Eq # 1
Ahora veamos la expresión para adquirir la corriente dentro del inductor durante el período de apagado del transistor, se puede determinar con la ayuda de la siguiente ecuación:
Io= Ipaquete- (Vout - VD) Toff / L
Nuevamente, sustituyendo ipk - io por Δi en la expresión anterior obtenemos:
Δi = (Vout - VD) Toff / L ------------------------------------- Eq # 2
La Eq # 1 y Eq # 2 se pueden usar para determinar los valores de la corriente de ondulación mientras el transistor está suministrando corriente al inductor, es decir, durante su tiempo de ENCENDIDO ... y mientras el inductor está drenando la corriente almacenada a través de la carga durante los períodos de apagado del transistor.
En la discusión anterior, obtuvimos con éxito la ecuación para determinar el factor de corriente (amperios) en un inductor reductor.
Determinación de voltaje
Ahora intentemos encontrar una expresión que pueda ayudarnos a determinar el factor de voltaje en un inductor reductor.
Dado que Δi es común tanto en la ecuación n. ° 1 como en la ecuación n. ° 2, podemos equiparar los términos entre sí para obtener:
(Vino - Vtrans - Vout) Ton / L = (Vout - VD) Toff / L
VinTon - Vtrans - Vout = VoutToff - VDToff
VinTon - Vtrans - VoutTon = VoutToff - VDToff
VoutTon + VoutToff = VDToff + VinTon - VtransTon
Vout = (VDToff + VinTon - VtransTon) / T
Reemplazando las expresiones Ton / T por el ciclo de trabajo D en la expresión anterior, obtenemos
Vout = (Vin - Vtrans) D + VD (1 - D)
Procesando más la ecuación anterior obtenemos:
Vout + VD = (Vin - Vtrans + VD) D
o
D = Vout - VD / (Vin - Vtrans - VD)
Aquí VD se refiere a la caída de voltaje en el diodo.
Cálculo del voltaje reductor
Si ignoramos las caídas de voltaje en el transistor y el diodo (ya que pueden ser extremadamente triviales en comparación con el voltaje de entrada), podemos recortar la expresión anterior como se indica a continuación:
Vout = DVin
La ecuación final anterior se puede utilizar para calcular el voltaje de reducción que puede preverse de un inductor en particular mientras se diseña un circuito convertidor reductor.
La ecuación anterior es la misma que la discutida en el ejemplo resuelto de nuestro artículo anterior ' cómo funcionan los convertidores de dólar .
En el próximo artículo aprenderemos cómo estimar el número de vueltas en un inductor Buck ... por favor, estad atentos.
Anterior: Cómo funcionan los convertidores de Buck Siguiente artículo: Circuito controlador de motor sin escobillas de alto voltaje